Informatics and Applications
2025, Volume 19, Issue 2, pp 2-8
ESTIMATION OF PARAMETERS OF A MIXTURE OF NORMAL MULTIVARIATE DISTRIBUTIONS WITH CONSTRAINTS ON COVARIANCE MATRICES
Abstract
The formulation and method of solving the problem of finding an estimate of the maximum likelihood of the parameters of a mixture of normal multidimensional distributions that allow excluding the occurrence of "infinitely" large values of the likelihood function are considered. It is proposed to condition the set of possible covariance matrices so that they do not become singular. To do this, a boundary 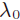 is introduced for the eigenvalues of the estimated covariance matrices of the elements of the mixture. Correction of small eigenvalues, smaller than is introduced for the eigenvalues of the estimated covariance matrices of the elements of the mixture. Correction of small eigenvalues, smaller than 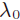 , covariance matrices of the elements of the mixture makes it possible to neutralize the arising computational problems with unlimited likelihood, however, at the cost of a rather laborious procedure for replacing the eigenvalues of covariance matrices, if necessary, at each step of the iterative EM (expectation-minimization) algorithm. The justification of the legitimacy of the proposed actions allows not only to obtain a detailed description of the corresponding actions but also to offer options for choosing a new additional parameter of the mixture elements, , covariance matrices of the elements of the mixture makes it possible to neutralize the arising computational problems with unlimited likelihood, however, at the cost of a rather laborious procedure for replacing the eigenvalues of covariance matrices, if necessary, at each step of the iterative EM (expectation-minimization) algorithm. The justification of the legitimacy of the proposed actions allows not only to obtain a detailed description of the corresponding actions but also to offer options for choosing a new additional parameter of the mixture elements,
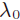 . Estimating mixture parameters under constraints primarily solves computational problems but can affect the efficiency of using mixture estimation. This is illustrated by the example of a data classification problem. . Estimating mixture parameters under constraints primarily solves computational problems but can affect the efficiency of using mixture estimation. This is illustrated by the example of a data classification problem.
[+] References (12)
- Krivenko, M. P. 2015. Modeli dlya predstavleniya i obrabotki referensnykh znacheniy [Models for representaion and treatment of reference values]. Informatika i ee Primeneniya — Inform. Appl. 9(2):63–74. doi: 10.14357/19922264150208.
- Krivenko, M. P. 2017. Mnogomernyy referensnyy region vysokoy plotnosti [High-density multivariate reference regions]. Informatika i ee Primeneniya - Inform. Appl. 11(2):59-64. doi: 10,14357/19922264170207,
- Krivenko, M. P. 2023, Kriterii vybora razmernosti modeli faktorizatsii [Criteria for choosing the factorization model dimensionality]. Informatika i ee Primeneniya - Inform. Appl. 17(2):50-56, doi: 10,14357/19922264230207,
- McLachlan, G., and D. Peel. 2000. Finite mixture models. Danvers, MA: Wiley. 464 p.
- McLachlan, G. J., and K. E. Basford. 1988. Mixture models: Inference and applications to clustering. New York, NY: Marsel Dekker. 273 p.
- Krivenko, M. P. 2007. Raspoznavanie elementov izobrazheniya, imeyushchikh razlichnye razmery [Recognition of image object with different picture size elements]. Sistemy i Sredstva Informatiki - Systems and Means of Informatics 17: 30-51.
- Seber, G. A. F. 2008, A matrix handbook for statisticians. Hoboken, NJ: Wiley. 560 p.
- Albert, A. 1987. Multivariate interpretation of clinical laboratory data. New York, NY: CRC Press. 386 p.
- Krivenko, M. P. 2019. Snizhenie razmernosti dlya smesi veroyatnostnykh analizatorov glavnykh komponent primenitel'no k zadacham meditsinskoy diagnostiki [Dimensionality reduction for mixture of probabilistic principal component analyzers in relation to the tasks of medical diagnostics]. Sistemy i Sredstva Informatiki - Systems and Means of Informatics 29(4):4-13.
- Chernick, M. R. 2008. Bootstrap methods: A guide for practitioners and reseachers. 2nd ed. Hoboken, NJ: Wiley. 370 p.
- Jones, E., S. Harden, and M. J, Crawley. 2023. The R book. 3rd ed. Hoboken, NJ : Wiley. 880 p.
- Chassagnol B., A. Bichat, C. Boudjeniba, P.-H. Wuillemin, M. Guedj, D. Gohel, G. Nuel, and E. Becht. 2023. Gaussian mixture models in R. R J. 15(2):56-76. doi: 10.32614/RJ-2023-043.
[+] About this article
Title
ESTIMATION OF PARAMETERS OF A MIXTURE OF NORMAL MULTIVARIATE DISTRIBUTIONS WITH CONSTRAINTS ON COVARIANCE MATRICES
Journal
Informatics and Applications
2025, Volume 19, Issue 2, pp 2-8
Cover Date
2025-07-10
DOI
10.14357/19922264250201
Print ISSN
1992-2264
Publisher
Institute of Informatics Problems, Russian Academy of Sciences
Additional Links
Key words
mixture of normal multivariate distributions; maximum likelihood estimate; EM-algorithm
Authors
M. P. Krivenko 
Author Affiliations
 Federal Research Center "Computer Science and Control" of the Russian Academy of Sciences, 44-2 Vavilov Str., Moscow 119333, Russian Federation
|