Informatics and Applications
2014, Volume 8, Issue 2, pp 70-76
ON POLYNOMIAL TIME COMPLEXITY OF ULTRAMETRIC VERSIONS OF CERTAIN NP-HARD PROBLEMS
Abstract
The paper deals with important special cases of the travelling salesman problem and the Steiner tree
problem. Both of these problems are NP-hard even in the metric case, i. e., for graphs whose edge cost function
meets the triangle inequality. Even more severe restriction is imposed by the strong triangle inequality:
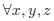
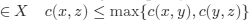
The function which meets this inequality is called ultrametric. The analysis
of graphs with an ultrametric edge cost function is presented. This analysis leads to an algorithm for building the
minimal cost Hamiltonian cycle in time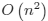 
where n is the number of vertices. For the Steiner tree problem, it
is proven that in the case of an ultrametric edge function, the minimumSteiner tree includes only terminal vertices
and thus may also be constructed in polynomial time, as a minimum spanning tree on a subgraph of the original
graph.
[+] References (10)
- Garey,M.R., andD. S. Johnson. 1979. Computers and intractability:
A guide to the theory of NP-completeness. New
York:W.H. Freeman & Co. New York. 338 p.
- Farach, M., S. Kannan, and T. Warnow. 1995. A robust
model for finding optimal evolutionary trees. Algorithmica.
Special Issue on Computational Biology. 13(1):155–179.
- Gusfield, D. 1997. Algorithms on strings, trees and
sequences: Computer science and computational biology.
Cambridge: Cambridge University Press. 556 p. http://
www.cs.ucdavis.edu/.gus¦eld/ultraerrat/ultraerrat.
html.
- Moore, N.C.A., and P. Proseer. 2008. The ultrametric
constraint and its application to phylogenetics. J. Artif.
Intell. Res. 32:901–938.
- Haubold, B., and T. Wiehe. 2006. Introduction to computational
biology: An evolutionary approach. 3rd ed. Basel:
Birkh.auser. 328 p.
- Li, X., C.G. Plaxton, M. Tiwari, and A. Venkataramani.
2004. Online hierarchical cooperative caching. 16th Annual
ACM Symposium on Parallelism in Algorithms and
Architectures (SPAA’04) Proceedings. New York. 74–83.
- Kintsel’ V. 1987. Spinovye stekla kak model’nye sistemy
dlya neyronnykh setey. [Spin glasses as model systems for
neural networks]. Uspekhi Fizicheskikh Nauk [Advances
in Physical Sciences] 152:123–131.
- Christofides, N. 1975. Graph theory: An algorithmic approach
(Computer science and applied mathematics). New
York: Academic Press. 400 p.
- Meinika, E. 1978. Optimization algorithms on networks and
graphs. New York–Basel: Dekker. 356 p.
- Bui, T.N., and C.M. Zrncic. 2006. An ant-based algorithm
for finding degree-constrained minimum spanning
tree. GECCO’06: 8th Annual Conference on Genetic and
Evolutionary Computation Proceedings. New York. 11–18.
[+] About this article
Title
ON POLYNOMIAL TIME COMPLEXITY OF ULTRAMETRIC VERSIONS OF CERTAIN NP-HARD PROBLEMS
Journal
Informatics and Applications
2014, Volume 8, Issue 2, pp 70-76
Cover Date
2014-03-31
DOI
10.14357/19922264140207
Print ISSN
1992-2264
Publisher
Institute of Informatics Problems, Russian Academy of Sciences
Additional Links
Key words
ultrametric function; strong triangle inequality; travelling salesman problem; Steiner tree; polynomialtime
algorithms
Authors
M.G. Adigeev 
Author Affiliations
Southern Federal University, 105/42 Bol’shaya Sadovaya Str., Rostov-on-Don 344006, Russian Federation
|